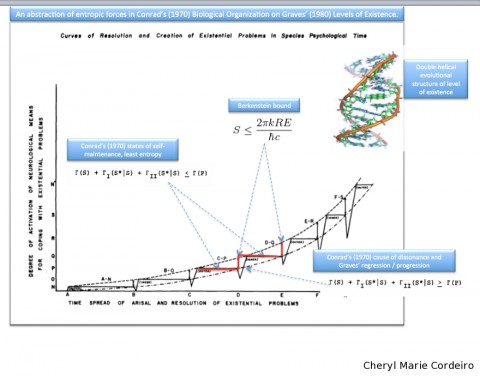
An abstraction of Michael Conrad’s (1970) Biological Organization on Clare W. Graves’ (1980) Levels of Existence.
Text and Photo © CM Cordeiro 2013
In reading about self-organizing structures for the relevance of theory applied to the field of international business (IB), I thought the ideas expressed by Michael Conrad in his paper entitled, Statistical and Hierarchical Aspects of Biological Organization (made accessible via NASA) was interesting when also applied to the theoretical constructs of Clare W. Graves’ Levels of Existence.
Conrad discusses the differentiation and uncertainty associated with the organization and variability in a biological organization’s compartmental structures, that are expressed in terms of certain entropy measures. In his paper, he tries to ascertain the most efficient operative level of a biological system, landing on the principle of static equilibrium that he uses vector models for representation.
I tried now in abstraction, to combine Conrad’s vector representations of states of self-maintenance and self-organization, to what I understand to be Clare W. Graves’ cyclic double-helical structure of evolution of human psychology and levels of existence.
Assume that the development of the Individual (and likewise Group) is dependent upon two entities, an internal biological coping mechanism, and external living conditions. The evolution of levels of existence, Graves suggests (Cowan & Todorovic 2005) is emergent, which one could thus assume in the context of quantum physics, that the emergent nature of these levels of existence are entropic, and could be stated via the Von Neumann entropy:
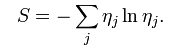
Or since there are two states, then the context could be expressed in joint quantum entropy:
![]()
According to Conrad (1970), what determines a state of close equilibrium or least entropy would be bounded entropies, expressed in the upper limit Bekenstein bound, that in abstraction, could be transposed to the upper bound of any of the 8 Gravesian levels of existence. The Bekenstein bound is expressed:
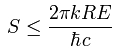
Conrad (1970:23ff) postulates that a self-organizing maintaining system will have an upper bound to the ensemble size, an abstraction that could be transposed to Gravesian stable values system in any one level of existence, stated as:
![]()
where the left hand side of the above equation should not only be as small a value as possible, but necessarily smaller than the right hand side. Once reversed:
![]()
would cause the dissonance of regression / progression in Gravesian Levels of Existence.
My thoughts are situated in the study of complex systems, including both physical and social systems that lead to the formulation of transformative / integrated frameworks of ideas and methods. Complex systems approaches help account for what were previously oversimplified classical science in the context of rapid advances in computational technologies, where insights gained from such studies are today being integrated into the working conceptual frameworks of many professions including engineering, medicine, finance, law and management in IB.
For the moment, my attention is drawn to the quantum and biological perspectives of complex systems that highlight the interdependence and co-evolution of systems, in this case, organizations that are self-organizing. This perspective would help corporate managers conceptualize their perspective on human capital management, turning towards facilitative management. Based on a network perspective of organizational behaviour between corporations, a complex systems perspective could also help companies leverage synergistic alliances in fine balance with competitive advantages.
Bibliography
- Jacobson, M. and Wilensky, U. 2006. Complex Systems in Education: Scientific and Educational Importance and Implications for the Learning Sciences. The Journal of the Learning Sciences 15(1): 11-14. Lawrence Erlbaum Associates, Inc.